Điện áp Hiệu Dụng Cực đại Giữa Hai Bản Tụ điện Và Gữa Hai đầu Cuộn …

Điện áp hiệu dụng cực đại giữa hai bản tụ điện và giữa hai đầu cuộn cảm là bài toán Open liên tục trong những kỳ thi trung học phổ thông Quốc gia, đề thi ĐH, đề thi tốt nghiệp trung học phổ thông những năm gần đây. Cứ cho là học viên đã được học và chỉ ngay ra được $ U_ { C_ \ text { max } } $ hay $ U_ { L_ \ text { max } } $ ( điện áp hiệu dụng cực đại giữa hai bản tụ và điện áp hiệu dụng cực đại giữa hai đầu cuộn cảm ), và chỉ ra được khi nào thì $ U_ { C_ \ text { max } } $, $ U_ { L_ \ text { max } } $, nhưng để xử lý được những yếu tố tương quan tiếp theo thì khá khó khăn vất vả và mất nhiều thời hạn. Chưa nói đến việc hầu hết học viên không nhớ được biểu thức tính $ U_ { C_ \ text { max } } $, $ U_ { L_ \ text { max } } $, rồi biểu thức điều kiện kèm theo để xảy ra $ U_ { C_ \ text { max } } $, $ U_ { L_ \ text { max } } USD. Mà có nhớ được thì việc vận dụng một vài công thức trong ” bát ngát bát ngát những sáng tạo độc đáo của người ra đề ” là rất khó khăn vất vả. Tóm lại, bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ và gữa hai đầu cuộn cảm vẫn thường được xếp hạng mức độ vận dụng cao. Tuy nhiên sau khi đọc xong bài viết này, chắc như đinh ai cũng phải thừa nhận rằng bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ và gữa hai đầu cuộn cảm thật là đơn thuần.

Giải bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ và gữa hai đầu cuộn cảm bằng đạo hàm sẽ lâu hơn và kết quả khó áp dụng cho những bài toán tiếp theo

Bài toán như sau: Cho mạch điện xoay chiều $RLC$, trong đó điện dung $C$ có thể thay đổi được. Tìm $C$ để điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại. Tính giá trị cực đại đó. (Bài toán về $L$ biến thiên ta ta suy luận tương tự). Bắt đầu thừ biểu thức tính điện áp hiệu dụng giữa hai bản tụ điện trong mạch RLC \begin{align} U_C&=IZ_C\\ &=\frac{U}{Z}Z_C\\ &=\frac{UZ_C}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}\\ &=\frac{U}{\sqrt{R^2\frac{1}{Z^2_C}+\left(\frac{Z_L}{Z_C}-1\right)^2}} \end{align} Đạo hàm biểu thức trong căn $$f\left(\frac{1}{Z_C}\right)=R^2\frac{1}{Z^2_C}+\left(\frac{Z_L}{Z_C}-1\right)^2$$ $$f’\left(\frac{1}{Z_C}\right)=\frac{2R^2}{Z_C}+2Z_L\left(\frac{Z_L}{Z_C}-1\right)\\ f’\left(\frac{1}{Z_C}\right)=0\\ \Rightarrow Z_C=\frac{R^2+Z_L^2}{Z_L}$$ Việc biến đổi này không khó, nhưng hơi dài và đòi hởi một chút kiên nhẫn. Nhưng tôi muốn nói đến kết quả chúng ta mới tìm được. Thứ nhất liệu học sinh có nhớ được nó cùng với bao nhiêu công thức khác hay không? Thứ hai, nếu nhớ được thì áp dụng nó cho các bài toán tiếp theo ra sao? Ví dụ như câu 33 đề minh họa 2022, khi đã có kết quả này rồi, ta phải tìm điện áp hiệu dụng cực đại trên $R$ như thế nào? Thôi không dài dòng nữa, chúng ta sẽ giải bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ và gữa hai đầu cuộn cảm này bằng một lời giải tuyệt vời sau đây.

Giải bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ điện và gữa hai đầu cuộn cảm bằng giản đồ véc-tơ

Cũng bài toán như trên, với mạch điện $ RLC $ như hình vẽ.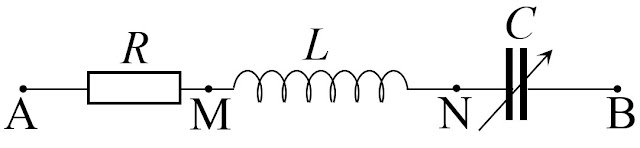

Ta vẽ giản đồ véc tơ một cách tổng quát

Trên giản đồ véc tơ, góc $ \ alpha USD không đổi, chính do $ Z_L $ và $ R $ không đổi. Ta vận dụng định lí hàm số sin \ begin { align } \ frac { U_C } { \ sin { \ beta } } = \ frac { U } { \ sin { \ alpha } } \ \ \ Rightarrow U_C = \ frac { U } { \ sin { \ alpha } } \ sin { \ beta } \ end { align } Vì $ U $ và $ \ sin { \ alpha } $ không đổi nên $ U_ { C_ \ text { max } } $ khi $ $ \ left ( \ sin { \ beta } \ right ) _ \ text { max } = 1 \ \ \ beta = 90 ^ 0 $ $ Tam giác $ ABN $ vuông tại USD A $. Điều này thật tuyệt vời, vì trong hình này, tổng thể những tam giác đồng dạng với nhau. Hệ thức liên hệ giữa những cạnh của những tam giác đồng dạng không có gì đơn thuần hơn., khi gặp bài toán tìm $ C $ để $ U_ { C_ \ text { max } } $ hoặc tìm $ L $ để $ U_ { L_ \ text { max } } $ thì ta chỉ cần vẽ giản đồ thành tam giác vuông như dưới đây : 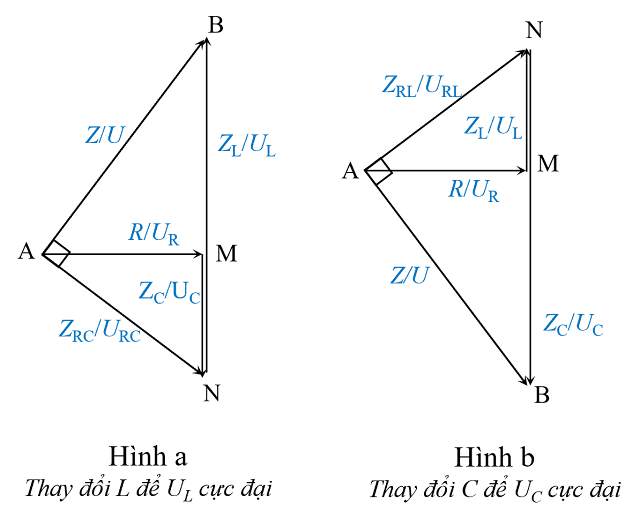Bài viết này không không có mục tiêu nêu cách giải bài toán Điện áp hiệu dụng cực đại giữa hai bản tụ điện và gữa hai đầu cuộn cảm, mà mục tiêu cao hơn là trình làng một công cụ tuyệt vời để giải một cách đơn thuần những bài tập khó tương quan đến mạch điện xoay chiều có \ ( C \ ) đổi khác hoặc \ ( L \ ) biến hóa để \ ( U_C \ ) hoặc \ ( U_L \ ) cực đại. Sự đơn thuần đó chính là bộ đôi tam giác vuông này. Thứ nhất, nó dễ nhớ hơn cái công thức $ Z_C = \ frac { R ^ 2 + Z_L ^ 2 } { Z_L } $ đã tìm được bằng đạo hàm. Thứ hai, bạn hoàn toàn có thể lấy ra từ những tam giác đồng dạng này hàng đống biểu thức khác nữa, chúng rất tiện cho những bài toán ở Lever cao hơn. Nào, giờ đây mới là mở màn …

Điện áp hiệu dụng cực đại giữa hai bản tụ điện và gữa hai đầu cuộn cảm và những bài toán liên quan

Bài toán 1. Điện áp hiệu dụng hai đầu cuộn cảm đạt cực đại

Đặt vào hai đầu mạch $RLC$ một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi, cố định $R$ và $C$, thay đổi $L$. Khi $Z_L = 90\ \text{Ω}$ thì điện áp hiệu dụng hai đầu tụ điện đạt cực đại, lúc đó tổng trở của mạch là $120\ \text{Ω}$. Tính tổng trở của mạch khi điện áp hiệu dụng hai đầu cuộn cảm đạt cực đại. Đặt vào hai đầu mạch $ RLC $ một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi, cố định và thắt chặt $ R $ và USD C $, biến hóa USD L USD. Khi $ Z_L = 90 \ \ text { Ω } $ thì điện áp hiệu dụng hai đầu tụ điện đạt cực đại, lúc đó tổng trở của mạch là USD 120 \ \ text { Ω } USD. Tính tổng trở của mạch khi điện áp hiệu dụng hai đầu cuộn cảm đạt cực đại .USD L $ đổi khác để $ U_C $ đạt cực đại, khi đó hiện tượng kỳ lạ cộng hưởng xảy ra $ $ Z_C = Z_L = 90 \ \ text { Ω } \ \ R = Z = 120 \ \ text { Ω } $ $ Khi $ U_L $ đạt cực đại, ta vận dụng Hình a ở trên với những tam giác đồng dạng ABN và MAN $ $ \ frac { AB } { AN } = \ frac { MA } { MN } \ \ \ text { hay } \ \ frac { Z } { R ^ 2 + Z_C ^ 2 } = \ frac { R } { Z_C } $ $ \ begin { align } \ Rightarrow Z và = \ frac { R } { Z_C } \ sqrt { R ^ 2 + Z_C ^ 2 } \ \ và = \ frac { 120 } { 90 } \ sqrt { 120 ^ 2 + 90 ^ 2 } \ \ và = 200 \ \ text { Ω } \ end { align }

Bài toán 2. Điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại

Mạch điện AB gồm AM chứa điện trở thuần không đổi, MN chứa cuộn dây cảm thuần có độ tự cảm không đổi và NB chứa tụ điện có điện dung thay đổi được. Đặt vào hai đầu AB điện áp xoay chiều có giá trị hiệu dụng $U = 100\ \text{V}$ và tần số không đổi. Điều chỉnh điện dung của tụ điện để điện áp hiệu dụng trên tụ điện đạt cực đại. Khi đó điện áp tức thời trên đoạn AN có biểu thức $u_\text{AN} = 100\sqrt{6}\cos{\left(100\pi t + \frac{\pi}{6}\right)}\ \text{V}$. Tính điện áp hiệu dụng trên tụ điện và viết biểu thức điện áp tức thời hai đầu cuộn cảm khi đó. Mạch điện AB gồm AM chứa điện trở thuần không đổi, MN chứa cuộn dây cảm thuần có độ tự cảm không đổi và NB chứa tụ điện có điện dung đổi khác được. Đặt vào hai đầu AB điện áp xoay chiều có giá trị hiệu dụng $ U = 100 \ \ text { V } $ và tần số không đổi. Điều chỉnh điện dung của tụ điện để điện áp hiệu dụng trên tụ điện đạt cực đại. Khi đó điện áp tức thời trên đoạn AN có biểu thức USD u_ \ text { AN } = 100 \ sqrt { 6 } \ cos { \ left ( 100 \ pi t + \ frac { \ pi } { 6 } \ right ) } \ \ text { V } USD. Tính điện áp hiệu dụng trên tụ điện và viết biểu thức điện áp tức thời hai đầu cuộn cảm khi đó .

Ý thứ nhất, ta tính điện áp hiệu dụng trên tụ điện như sau: Từ Hình b, ta xét tam giác vuông ABN để rút ra \begin{align} NB& = AB^2 + NA^2\\ \text{hay}\ U_C&= \sqrt{U^2 + U^2_\text{AN}}\\ &= \sqrt{100^2 + \left(100\sqrt{3}\right)^2}\\ &= 200\ \text{V} \end{align} Ý thứ hai, ta phải lập biểu thức điện áp tức thời trên cuộn dây \begin{align} \frac{U_L}{U_\text{AN}} & = \frac{U_\text{AN}}{U_C}\\ U_L& = \frac{U_\text{AN}^2}{U_C}\\ &= \frac{\left(100\sqrt{3}\right)^2}{200}\\ &= 150\ \text{V} \end{align} Đặt góc $\hat{ANB} = α$ thì \begin{align} \tan{α}& = \frac{U}{U_\text{AN}}\\ &= \frac{100}{100\sqrt{3}}\\ &= \frac{1}{\sqrt{3}}\\ α &= \frac{\pi}{6} \end{align} Như vậy $u_L$ nhanh pha hơn $u_\text{AN}$ một góc $α = \frac{\pi}{6}$, phương trình cần tìm là \begin{align} u_L &= 150\sqrt{2}\cos{\left(100\pi t + \frac{\pi}{6} + \frac{\pi}{6}\right)}\\ &= 150\sqrt{2}\cos{\left(100\pi t + \frac{\pi}{3}\right)}\ \text{V} \end{align}

Xem thêm: Bán Linh Kiện Điện Tử Giá Rẻ Nhất Tại Tphcm

Bài toán 3. Điện áp hiệu dụng giữa hai bản tụ điện đạt cực đại

Trong mạch $RLC$ có $R$ và $L$ không đổi. Đặt hai đầu mạch vào điện áp xoay chiều có giá trị hiệu dụng không đổi và thay đổi điện dung $C$ của tụ điện. Khi dung kháng của tụ điện có các giá trị $70\ \text{Ω}$ và $110\ \text{Ω}$ thì điện áp hiệu dụng trên cuộn dây có cùng giá trị. Khi dung kháng bằng $120\ \text{Ω}$ thì điện áp hiệu dụng trên tụ điện đạt cực đại và biểu thức điện áp tức thời trên tụ điện là $u_C = 220\sqrt{2}\cos{\left(100\pi t + \frac{\pi}{2}\right)}\ \text{V}$, biểu thức điện áp tức thời trên đoạn mạch chỉ có $R$ và $L$ là A. $u_{RL} = 110\sqrt{6}\cos{\left(100\pi t – \frac{2\pi}{3}\right)}\ \text{V}.$ B. $u_{RL} = 110\sqrt{3}\cos{\left(100\pi t + \frac{4\pi}{3}\right)}\ \text{V}.$ C. $u_{RL} = 110\sqrt{6}\cos{\left(100\pi t – \frac{4\pi}{3}\right)}\ \text{V}.$ D. $u_{RL} = 110\sqrt{3}\cos{\left(100\pi t + \frac{\pi}{3}\right)}\ \text{V}.$ Trong mạch $ RLC $ có $ R $ và $ L $ không đổi. Đặt hai đầu mạch vào điện áp xoay chiều có giá trị hiệu dụng không đổi và biến hóa điện dung $ C $ của tụ điện. Khi dung kháng của tụ điện có những giá trị USD 70 \ \ text { Ω } $ và USD 110 \ \ text { Ω } $ thì điện áp hiệu dụng trên cuộn dây có cùng giá trị. Khi dung kháng bằng USD 120 \ \ text { Ω } $ thì điện áp hiệu dụng trên tụ điện đạt cực đại và biểu thức điện áp tức thời trên tụ điện là USD u_C = 220 \ sqrt { 2 } \ cos { \ left ( 100 \ pi t + \ frac { \ pi } { 2 } \ right ) } \ \ text { V } $, biểu thức điện áp tức thời trên đoạn mạch chỉ có $ R $ và $ L $ là USD u_ { RL } = 110 \ sqrt { 6 } \ cos { \ left ( 100 \ pi t – \ frac { 2 \ pi } { 3 } \ right ) } \ \ text { V }. $ $ u_ { RL } = 110 \ sqrt { 3 } \ cos { \ left ( 100 \ pi t + \ frac { 4 \ pi } { 3 } \ right ) } \ \ text { V }. $ $ u_ { RL } = 110 \ sqrt { 6 } \ cos { \ left ( 100 \ pi t – \ frac { 4 \ pi } { 3 } \ right ) } \ \ text { V }. $ $ u_ { RL } = 110 \ sqrt { 3 } \ cos { \ left ( 100 \ pi t + \ frac { \ pi } { 3 } \ right ) } \ \ text { V }. $

Đầu tiên, ta giải quyết cái ý: Khi dung kháng của tụ điện có các giá trị $70\ \text{Ω}$ và $110\ \text{Ω}$ thì điện áp hiệu dụng trên cuộn dây có cùng giá trị. Ý này nên giải quyết bằng cách áp dụng định lí Viet (tham khảo ở đây: ỨNG DỤNG ĐỊNH LÍ VIET CHO CÁC BÀI TOÁN VẬT LÝ) Ta đưa biểu thức tính $U_L$ về dạng phương trình bậc hai biến $Z_C$ \begin{align} U_C&=IZ_L\\ &=\frac{UZ_L}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}\\ \end{align} $$Z_C^2-2Z_LZ_C+R^2+Z_L^2\left(1-\frac{U^2}{U_L^2}\right)=0$$ Định lí Viet cho các hệ số $a=1$, $b=-2Z_L$, $c=R^2+Z_L^2\left(1-\frac{U^2}{U_L^2}\right)$ như sau: $$Z_{C_1}+Z_{C_2}=-\frac{-2Z_L}{1}$$ \begin{align} Z_L&=\frac{Z_{C_1}+Z_{C_2}}{2}\\ &=\frac{70+110}{2}\\ &=90\ \text{Ω} \end{align} Bây giờ, ta sẽ xét đến tình huống: Khi dung kháng bằng $120\ \text{Ω}$ thì điện áp hiệu dụng trên tụ điện đạt cực đại và biểu thức điện áp tức thời trên tụ điện là $u_C = 220\sqrt{2}\cos{\left(\pi t + \frac{\pi}{2}\right)}\ \text{V}$. Chẳng cần suy nghĩ gì, vẽ ngay tam giác vuông như Hình b ở trên.

Xem thêm: Flycam giá rẻ nên mua loại nào – Linh kiện RC

Tại đây ta đã có $ Z_C = NB = 120 \ \ text { Ω } $, $ Z_L = MN = 90 \ \ text { Ω } $, bằng hệ thức những tam giác đồng dạng tính được $ Z_ { RL } = AN $ để suy ra $ U_ { RL } $, góc lệch pha so với USD u_C USD là $ \ left ( \ vec { AN }, \ vec { NB } \ right ) = \ pi – \ alpha USD từ đó viết phương trình USD u_ { RL } USD. Trình tự như sau : \ begin { align } \ frac { Z_ { RL } } { 90 } và = \ frac { 120 } { Z_ { RL } } \ \ Z_ { RL } và = \ sqrt { 120 \ times90 } \ \ và = 60 \ sqrt { 3 } \ \ text { Ω } \ end { align } Điện áp hiệu dụng trên đoạn mạch $ RL $ là \ begin { align } U_ { RL } và = IZ_ { RL } \ \ và = \ frac { U_C } { Z_C } \ times Z_ { RL } \ \ và = \ frac { 220 } { 120 } \ times60 \ sqrt { 3 } \ \ và = 110 \ sqrt { 3 } \ \ text { V } \ \ \ cos { \ alpha } và = \ frac { Z_ { RL } } { Z_C } \ \ và = \ frac { 60 \ sqrt { 3 } } { 120 } \ \ và = \ frac { sqrt { 3 } } { 2 } \ \ \ alpha và = \ frac { \ pi } { 6 } \ end { align } Điện áp USD u_ { RL } $ ( ứng với $ \ vec { AN } $ ) nhanh pha hơn điện áp giữa hai bản tụ USD u_C USD ( ứng với $ \ vec { NB } $ ) một góc $ $ \ pi – \ alpha = \ frac { 5 \ pi } { 6 } $ $ Phương trình điện áp tức thời trên đoạn mạch $ RL $ là \ begin { align } u_ { RL } và = 110 \ sqrt { 3 } \ sqrt { 2 } \ cos { \ left ( 100 \ pi t + \ frac { \ pi } { 2 } + \ frac { 5 \ pi } { 6 } \ right ) } \ \ và = 110 \ sqrt { 6 } \ cos { \ left ( 100 \ pi t + \ frac { 4 \ pi } { 3 } \ right ) } \ \ text { V } \ end { align } Đến đây ta so sánh với những giải pháp đưa ra của câu hỏi, thì thấy pha khởi đầu không trùng với giải pháp nào. Với giá trị một góc nào đó, hãy bình tĩnh xem lại bằng đường tròn lượng giác nhé. Rõ ràng điểm pha ứng với cung $ \ frac { 4 \ pi } { 3 } $ trùng với USD – \ frac { 2 \ pi } { 3 } USD. Tức là giải pháp A là giải pháp đúng. Chuyên mục : Chuyên đề dạy học vật lí, Chuyên đề vật lí 12, Ôn thi đại học, Chuyên đề dạy học vật lí, Chuyên đề vật lí 12, Ôn thi ĐH ,

Source: https://dichvubachkhoa.vn
Category : Linh Kiện Và Vật Tư